3.3 Краткая историческая справка

Рассматриваемая пропорция получила название "золотое деление" от Леонардо да Винчи, искавшего гармонические отношения в живописи, архитектуре, строении человеческого тела, всерьез интересовавшегося и математикой. Другие названия: золотое сечение, гармоническое деление, деление в крайнем и среднем отношении [199]. Один из близких друзей Леонардо, крупнейший европейский алгебраист ХV в. итальянец Лука Пачоли,(1) написал по его настоянию книгу "О божественной пропорции" (De divina proportione, 1497, изд. в Венеции в 1509 г.), увидев в золотом сечении божественные черты. Такая пропорция лишь одна, а единственность - высочайшее свойство Бога. В ней воплощено святое триединство. Эта пропорция не может быть выражена доступным числом, остается скрытой и тайной и самими математиками называется иррациональной (так и Бог не может быть ни определен, ни разъяснен словами). Бог никогда не изменяется и представляет всё во всем и всё в каждой своей части, так и золотое сечение для всякой непрерывной и определенной величины (независимо от того, большая она или малая) одно и то же, не может быть ни изменено, ни по иному воспринято рассудком. Бог вызвал к бытию небесную добродетель, иначе называемую пятой субстанцией, с ее помощью и четыре других простых тела (четыре стихии - землю, воду, воздух, огонь), а на их основе вызвал к бытию всякую другую вещь в природе; так и наша священная пропорция, согласно Платону в "Тимее", дает формальное бытие самому небу, ибо ему приписывается вид тела, называемого додекаэдром, который невозможно построить без золотого сечения. Таковы аргументы Пачоли [329].

Но само золотое сечение было известно задолго до Ренессанса. В работе Пачоли изложение велось по так называемой ХIV книге "Начал" Эвклида (на самом деле Гипсикла). В книге II "Начал" встречается построение, равносильное уравнению (4). В книгах IV и ХIV золотое деление применяется для построения правильных пяти- и десятиугольников; в стереометрии - правильных двенадцатигранников (додекаэдров) и двадцатигранников (икосаэдров). Считают, такие геометрические процедуры были известны еще пифагорейцам,(2) далее след золотого сечения теряется, возможно, в Египте. Многомудрые греки сочли разумным возвести генезис пропорций к самим истокам вселенной: "По Ферекиду, Зевс связал определенными пропорциями то, что прежде было хаотично" [370, c. 159].

По традиции, золотое сечение вводится в геометрии через построение правильных пятиугольников, как выпуклых, так и звездчатых (т.е. пятиконечной звезды). Придерживается этой тактики и немецкий профессор Г.Е.Тимердинг, написавший в первой четверти ХХ века книгу о золотом сечении. Он констатирует: "У пифагорейцев <...> с правильным пятиугольником была связана мысль о таинственных силах и свойствах, но эти свойства обнаруживаются лишь тогда, когда рядом с обыкновенным правильным пятиугольником будет рассматриваться та звезда, которая получается при последовательном соединении через одну всех вершин обыкновенного пятиугольника, составленная диагоналями пятиугольника" [329, c. 11; см. рис. 5], - и далее отмечает: пентаграмма играла большую роль во всех магических науках. "Во многих местностях она употреблялась народом в виде "ведьминой стопы" (Drudenfuss), как средство защиты от злых духов, в частности, для охраны спящего от ведьм и от производимого ими кошмара" [там же]. Пентаграммой пользовался и Фауст в трагедии Гёте.

Рис. 3-5

Пятиконечная звезда, как показывает Тимердинг, буквально нашпигована пропорциями золотого сечения. Пифагореец Тимей в одноименном диалоге Платона говорит: "Невозможно, чтобы две вещи совершенным образом соединились без третьей, так как между ними должна появиться вещь, которая скрепляла бы их. Это наилучшим образом может выполнить пропорция, ибо если три числа обладают тем свойством, что среднее так относится к меньшему, как большее к среднему, и, наоборот, меньшее так относится к среднему, как среднее к большему, то последнее и первое будет средним, а среднее - первым и последним. Таким образом, все необходимое будет тем же самым, а так как оно будет тем же самым, то оно составит целое". Земной мир Платон строит, используя треугольники двух сортов: равнобедренные и неравнобедренные. Прекраснейшим прямоугольным треугольником он считает такой, в котором гипотенуза вдвое больше меньшего из катетов (такой прямоугольник является половиной равностороннего, основной фигуры вавилонян, в нем выступает отношение 1 : √3, отличающееся от золотого сечения примерно на 1/25, и называемое Тимердингом "соперником золотого сечения"). С помощью треугольников Платон строит четыре правильных многогранника, ассоциируя их с четырьмя земными элементами (землей, водой, воздухом и огнем). И лишь последний из пяти существующих правильных многогранников - додекаэдр, всеми двенадцатью гранями которого служат правильные пятиугольники, претендует на символическое изображение небесного мира.

Честь открытия додекаэдра (или, как полагалось, самой Вселенной, этой квинтэссенции четырех стихий, символизируемых, соответственно, тетраэдром, октаэдром, икосаэдром и кубом) принадлежит Гиппасу, впоследствии погибшему при кораблекрушении.(3) В этой фигуре действительно запечатлено множество отношений золотого сечения, поэтому последнему отводилась главная роль в небесном мире [329, c. 53], на чем впоследствии и настаивал брат минорит Лука Пачоли.

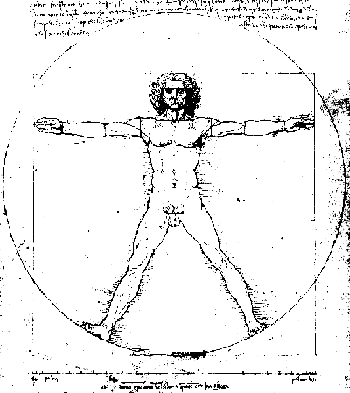
В средние века пентаграмма подверглась демонизации(4) (как, впрочем, и многое, что почиталось божественным в античном язычестве) и нашла приют в оккультных науках. Однако Возрождение вновь выносит на свет и пентаграмму, и золотое сечение. Так, широкое хождение в тот период утверждения гуманизма обрела схема, описывающая строение человеческого тела:

Рис. 3-6

К такой картинке, по сути воспроизводящей пентаграмму 3-5, неоднократно прибегал и Леонардо да Винчи. Ее интерпретация: тело человека обладает божественным совершенством, ибо заложенные в нем пропорции - такие же, как в главной небесной фигуре.(5)

Так как я не числю себя экспертом ни в тайных науках, ни в теологии, ни в метафизике, в дальнейшем не будут затрагиваться "трансцендентные" интерпретации пентаграмм, их связь с небесным или инфернальным мирами. В центре внимания останутся куда более обыденные, позитивные свойства пропорции, ее связь с массовым сознанием и политикой ХХ в. Хотя в государственную символику двух сверхдержав и входили пятиконечные звезды, оставим историкам честь возводить их генезис к масонам, т.е. к паранаукам; у нас же вопрос о влиянии этого факта на коллективное сознание или о том, какие черты последнего нашли воплощение в данном геометрическом символе, оставлен за скобками.

В очередной раз интерес к золотому сечению вспыхнул во второй половине ХIХ - начале ХХ вв. Тот же Тимердинг ссылается на предшественников: на Цейзинга,(6) полагавшего, что построение частей в отношении золотого сечения есть "вообще основной принцип всякого созидания, стремящегося к красоте и цельности, как в царстве природы, так и в области искусства" [329, c. 57], на Франса Ксавера Пфайфера,(7) приводившего фотографические снимки объектов природы и результаты их измерений, на Г.Т.Фехнера,(8) а также на опыты Витмера (Witmer, 1894) и Сегала (Segal, 1906). "Для картин с ясно изображенным горизонтом, у которых расстояние между двумя параллельными линиями, а именно между верхним и нижним краем картины, должно быть разделено третьей параллелью - горизонтом, с давних пор установлено правило, что это деление должно производиться по золотому сечению" [329, c. 66]. Например, если на картине изображены море и небо (следовательно, и разделяющий их горизонт), то одно должно перевешивать, т.к. видовое различие между ними влечет за собой подчеркивание одной или другой части. Одному отдается предпочтение, но избегая преувеличения. Поиск среднего пути между равенством и преувеличением приводит к определенной пропорции, в результате чего мы обретаем спокойствие, уверенность, впечатление чего-то закрепленного в самом себе. Форматам книг, картинам, входным билетам, бумажникам, сундукам, шоколадным плиткам, пересказывает Тимердинг, часто придается форма, соответствующая золотому сечению (отношение сторон прямоугольника равно соответствующей величине). Опыты с людьми по выбору из десяти прямоугольников разной формы показывали заметное предпочтение золотого сечения.

Впрочем, сам Тимердинг, как рациональный ученый, значительно осторожнее: "Гораздо более правдоподобным является предположение, что золотому сечению первоначально было отдано предпочтение по рассудочным соображениям. Но вследствие того, что это отношение было избрано нормой для бесчисленного множества употребляемых форм и что его приближения, естественно получающиеся путем выбора удобных близких численных соотношений, в общем и целом выдвигаются снова, оно в конце концов так утвердилось в представлении, что даже бессознательный выбор отношения размеров тоже тяготеет к нему" [329, c. 73].

Древние принципы соразмерности действуют как в живописи, так и в архитектуре: от Вавилона (в котором, напомним, роль главной фигуры играл равносторонний треугольник и благодаря ему отношение 1 : √3 ), Малой Азии, Греции, через искусство рисования и архитектурную готику европейских Средних веков до эпохи Леонардо да Винчи и Дюрера.(9) У египтян и вавилонян соотношение размеров в храме имело священное значение. Витрувий (III, гл.1), которому следовал Лука Пачоли в изложении архитектурных вопросов, выдвигал требование "симметрии" (теперь это слово употребляется в совсем другом смысле). Симметрия происходит от пропорции, которая по-гречески называется "аналогией". Пропорциональность означала при этом "согласованность соответствующих частей постройки между собой и целым". Архитекторам надлежит в совершенстве владеть учением о симметрии. При построении отдельных частей пользуются одним и тем же отношением, обнаруживающимся у целого.

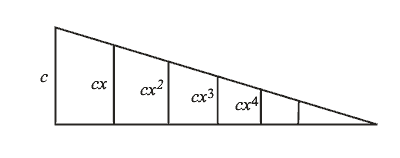
Тимердинг приводит математическую расшифровку: части постройки должны быть членами геометрической прогрессии

Ее графическое изображение:

Рис. 3-7

В частном случае, когда прогрессия (13) является возвратной, т.е. когда первый член и, следовательно, каждый другой равен сумме двух последующих,(10) получаем с = сx + сx², или 1 = x + x², что повторяет уравнение для золотого сечения (7).

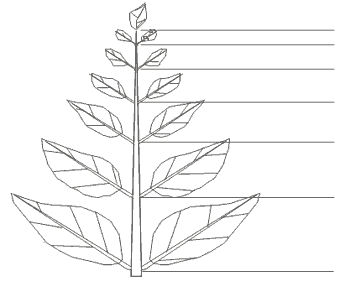
Сходным образом, отталкиваясь от Цейзинга, Тимердинг интерпретирует и природные явления, в частности закон листорасположения:

Рис. 3-8

Так, Тимердинг утверждает: "К тому же в природе, по-видимому, действительно выполняется некоторый закон пропорций, не совпадающий, правда, с отношением золотого сечения, но, так сказать, одного с ним направления. Этот закон можно так сформулировать: когда однородные части следуют друг за другом в порядке убывания величины, если нет возмущающих влияний, уменьшение происходит в геометрической прогрессии; так же происходит и увеличение там, где величина частей возрастает" [329, c. 58]. Направление в природных объектах задано ростом, и более старые части, из которых вырастают новые, оказываются либо самыми маленькими, либо, наоборот, самыми большими. Этот закон назвали законом натурального роста. Там, где он соблюдается, может встретиться и отношение золотого сечения, если не точное, то приближенное.

Выше уже упоминалось о связи золотого сечения с числами Фибоначчи. Н.Н.Воробьев уточняет и дополняет сказанное Тимердингом: "Природа дает нам многочисленные примеры расположения однородных предметов, описываемых числами Фибоначчи. В разнообразных спиралевидно расположенных мелких частях растений обычно можно усмотреть два семейства спиралей. В одном из этих семейств спирали завиваются по часовой стрелке, в другом - против. Числа спиралей того и другого типов часто оказываются соседними числами Фибоначчи. Так, взяв сосновую веточку, легко заметить, что хвоины образуют две спирали, идущие справа внизу налево вверх. Вместе с тем они же составляют три спирали, идущие слева снизу направо вверх. На многих шишках семена (т.е. "чешуйки") расположены в трех спиралях, полого навивающихся на стержень шишки. Они же расположены в пяти спиралях, круто навивающихся в противоположном направлении. В крупных шишках удается наблюдать 5 и 8 и даже 8 и 13 спиралей. Хорошо заметны такие спирали и на ананасе: обычно их бывает 8 и 13. У многих сложноцветных (например, у маргаритки или ромашки) заметно спиральное расположение отдельных цветков в соцветиях-корзинках. Число спиралей бывает здесь 13 в одном направлении и 21 в другом и даже соответственно 21 и 34. Особенно много спиралей можно наблюдать в расположении семечек крупного подсолнуха. Их число в каждом из направлений может достигать соответственно 55 и 89" [86, c. 122].

В книге Н.Н.Воробьева обсуждается вопрос и непосредственно о золотом сечении. Приведем две цитаты: "Выдающийся геометр и астроном ХVII века И.Кеплер (известный, впрочем, в свое время больше как астролог) отваживался даже ставить формулировку закономерности золотого сечения на один уровень с таким фундаментальным математическим фактом, как теорема Пифагора" [там же, с. 123]. И на той же странице: "Различными философами древности и средневековья внешняя красота прямоугольников и треугольников золотого сечения, а также других фигур, в которых наблюдается деление в среднем и крайнем отношении, возводилась в эмпирический и даже философский принцип. Золотым сечением и еще некоторыми отношениями пытались не только описывать, но и объяснять явления природы и даже общественной жизни, а с самим числом α (11) и его подходящими дробями производились разного рода мистические операции. Важную роль в таких рассмотрениях играла фигура, изображенная на рис. 3-5, которая при этом называлась пентаграммой". Далее Н.Н.Воробьев говорит о современном возрождении интереса к золотому сечению, в целом оценивая данный факт как негативный (что, впрочем, не помешало автору уделить значительное внимание этой теме в собственной брошюре). В России вопрос о золотом сечении, помимо Н.Н.Воробьева, затрагивался, например, в книге Е.И.Игнатьева "В царстве смекалки, или Арифметика для всех" [136].

Не следует полагать, что значение закономерности золотого сечения сводится исключительно к миру природы или изобразительных искусств. Так, Р. Якобсон обнаруживает образцы той же формы в литературе. Анализируя стихотворение Гельдерлина, он пишет о "многостороннем противопоставлении трех заключительных строк пяти предшествующим - одном из показателей сложного и преднамеренного формообразования. В последнем "Die Aussicht" Гельдерлина с полной отчетливостью представлено то самое золотое сечение, которое установилось со времен Леонардо. Меньший отрезок (Minor) относится к большему (Major) как больший к целому. Золотое сечение (8 : 5 = 5 : 3) противопоставляет неравные отрезки восьмистишия <...>" [402, c. 376]. Таким образом, попутно Якобсон использует и представление гармонической пропорции через числа Фибоначчи: здесь 3, 5, 8, см. ряд (12). Исследованию смысла той же пропорции, ее роли в искусстве, в частности, в музыке, уделял внимание и А.Ф.Лосев, см. [190, c. 356-368].(12) О "стремлении к гармонии имеющихся соотношений целого и его составных частей", о регулирующем правиле золотого сечения, последовательности Фибоначчи начинают говорить и современные политологи, см., напр., [330, c. 55].

На этом ограничим исторический экскурс. По-видимому, он полезен не только из прагматических соображений ("оживление материала"), но так или иначе обозначает позиции, которым придется следовать или, напротив, от которых отталкиваться в процессе дальнейшего изложения. Так, в целом для нас неприемлем, как сказано, ореол "духоведческих", оккультных истолкований, которыми оброс или из которых еще не окончательно вычленился рациональный феномен золотого сечения. Подобные коннотации, если и значимы в настоящем контексте, то лишь настолько, насколько массовым представлениям вообще присуще смешивать здравые начала с "загадочными", непросветленными критическим рассудком. Неудовлетворителен, на наш взгляд, и чисто позитивистский, голо-эмпирический путь, скажем, Цейзинга, Фехнера. Сами по себе опытные измерения не в состоянии подтвердить актуальности золотого сечения в природных явлениях, искусстве, в коллективных предпочтениях, ибо отсутствует действительно строгий критерий для того, чтобы отличить гармоническую пропорцию от других, ей близких. В результате выбор авторами именно золотого деления оставляет впечатление произвольности, недосказанности. Только соединение теории с опытом способно дать то сочетание логической обязательности и фактической подтвержденности, которое отличает науку в собственном смысле.

И в двух первых разделах главы, и в нижеследующих мы стараемся придерживаться именно этой линии. Очень важно, чтобы закономерность золотого сечения (или некие другие, ибо золотым сечением, в чем позже предстоит убедиться, существо вопроса не ограничивается) не оказывалась навязанной какими-то посторонними соображениями, а была необходимым, последовательным результатом содержательной теоретической модели политических систем, отчего в наше распоряжение автоматически попадал бы и ответ на вопрос "почему". (Очевидно, потому, что составные элементы системы обладают сформулированными в теории свойствами.) Теория, конечно, должна проверяться на практике, и в этом мы полностью солидарны с Цейзингом, Фехнером.

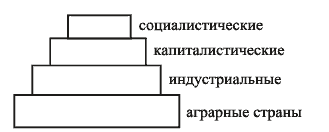
Вызывает интерес упомянутый Тимердингом "закон натурального роста". Не берусь судить о его общей формулировке, но в социально-политической сфере он находит определенные выражения. Так, если считать направлением исторического развития, или роста, движение от аграрных обществ к индустриальным, затем к разделению последних на капиталистические и социалистические, то каждая последующая ступень должна быть меньше предыдущей, образуя нечто вроде ступенчатой пирамиды:

Рис. 3-9

В послевоенном мировом сообществе отношение характеристических объемов четвертой ступени к третьей и, соответственно, третьей ко второй составляли значения, близкие к золотому делению. При этом, правда, остается неясным, существовали ли общие критерии оценки, вернее самооценки, у индустриального мира в целом, с одной стороны, и аграрного, с другой (признак объема промышленной продукции аутентичен лишь для индустриальных государств, но не для аграрных), поэтому трудно сказать что-либо конкретное о числовом соотношении между ними и даже о том, уместны ли вообще в данном случае количественные сравнения. Поэтому на стыке двух первых ступеней названный закон носит лишь описательный, полуметафорический характер.

Однако строение СССР (рис. 3-2, 3-3) в более строгом смысле соответствует названному закону. Именно вокруг РСФСР были объединены национальные окраины, ставшие, таким образом, следующей ступенью социалистического роста или процесса. Впоследствии отношение характеристических объемов "нацреспублики / РСФСР" установилось, как мы помним, вблизи значения, соответствующего золотому сечению. В свою очередь, если общим фундаментом или "корнем" обеих ступеней - и РСФСР, и нацреспублик - считать СССР ("идею СССР"), то и его объем удовлетворял условию (10). Обозначив характеристический объем СССР через с, придем к последовательности типа (13):

где х » 0,62 - величина, отвечающая золотому сечению, сх - объем РСФСР, сх² - нацреспублик.

Такие соображения наводят на мысль, что конструктивно-технологические начала в политике, возможно, не столь далеко отстоят от "органических", или естественно-исторических. Природа тоже строит свои "пирамиды".

Примечания

¹ После вступления во францисканский монашеский орден получил имя брата Луки из Борго Сан Сепольеро. Профессор математики в университете и других учебных заведениях Рима, Неаполя, Милана, Флоренции, Болоньи [142, c. 286 ].

² "Интерес пифагорейцев к симметрии, гармонии, числовым пропорциям привел их к занятиям "золотым делением" (выяснение правильных количественных соотношений между различными частями зданий или скульптурных фигур)", - пишет К.Куманецкий [169, c. 77].

³ В поздней древнегреческой легенде его смерть считалась наказанием за раскрытие тайны богов, "поскольку несказанное и безoбразное всегда должны пребывать сокрытыми". Ямвлих: "О Гиппасе говорят, что он был из числа пифагорейцев; за то, что разгласил и построил впервые сферу из двенадцати пятиугольников, он погиб в море как нечестивец, зато снискал славу первооткрывателя" [347, c. 152].

⁴ Чтобы подчеркнуть демоническое происхождение звездчатой пентаграммы, ее переворачивали "вверх ногами", в результате чего ее очертания напоминали два рога, два уха и козлиную бороду сатаны (этой разновидностью пользуются и современные сатанисты).

⁵ Хвост возрожденческой метафизики дотягивается до современности, и новейшие, насквозь коммерциализированные и абсолютно далекие, казалось бы, от высоких соображений модельно-подиумные стандарты диктуют для женской фигуры цифры 90 : 60 : 90, т.е. окружность талии должна составлять 2/3 от окружности бедер и груди. Как мы помним, 2/3 - второе из наилучших приближений к золотому сечению, см. ряд (12).

⁶ Zeising. Neue Lehre von den Proportionen des menschlichen Korpers. Leipzig, 1854 (Новое учение о пропорциях человеческого тела).

⁷ Franz Xaver Pfeifer. Der Goldene Schnitt. Augsburg, 1885 (Золотое сечение).

⁸ G.Th.Fechner. Vorschule der Aesthetik. 12A. 1897 (Введение в эстетику).

⁹ Основоположник живописи немецкого Возрождения А.Дюрер одновременно был и теоретиком искусства. В "Четырех книгах о пропорциях человека" (1528), составившим итог, или венец, его творчества, указано множество соотношений размеров правильных человеческих тел и лиц, совпадающих с пропорцией золотого сечения.

¹⁰ Или предыдущих - в зависимости от порядка расположения членов прогрессии.

¹¹ Такой буквой здесь обозначена величина α = (1 + √5 )/2

¹² В примечаниях к работе А.Ф.Лосева приведены ссылки на некоторую литературу, например, [201], [202] и о "золотом делении" у И.С.Баха: [439], [440]

назад | к началу сайта | к началу блока | вперед